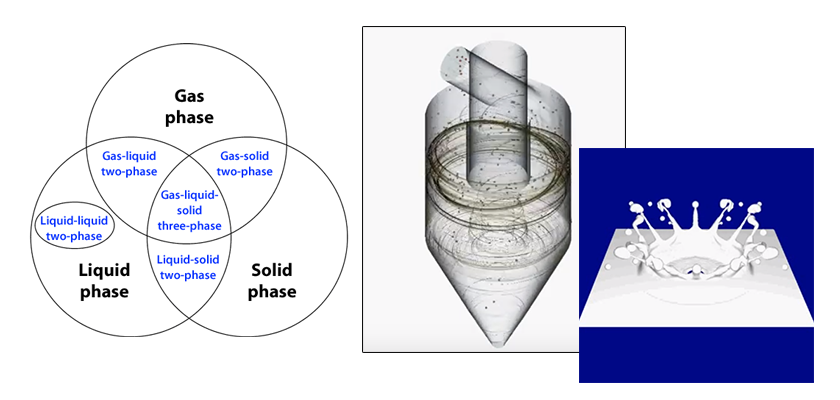
Column: Multiphase
New order | Old order


Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 21. Boiling flow analysis (free surface flow analysis with phase change)

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 20. Cavitation flow analysis

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 19. Solidification/melting analysis III

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 18. Solidification/melting analysis II

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 17. Solidification/melting analysis I

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 16. Dew condensation analysis III

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 15. Dew condensation analysis II

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 14. Dew condensation analysis I

Master Course for Fluid Simulation Analysis of Multi-phase Flows by Oka-san: 13. Analysis example – Chocolate fountain
Picked Up Contents
Whitepaper
Turbocharging CFD with Katana
Unleashing cutting-edge computational fluid dynamics from Japan


