Cavitation flow analysis

Cavitation flow analysis is an example of gas-liquid two-phase flow analyses. Cavitation is a phenomenon in which steam cavities are generated and disappear in an area in which the pressure of a liquid flowing at a high speed becomes equal to or less than the vapor pressure. It causes many challenges such as performance deterioration, vibration, noise, and damage (erosion) to fluid machinery including pumps, ship propellers, and liquid valves.

For a micro approach of cavitation flow analysis, a variety of modeling such as bubble generation, collapse, expansion, contraction, coalescence, and division on the order of μm is required. Unfortunately, it is difficult in the current fluid simulation analyses. Therefore, consider macro approaches instead.

As shown in Figure 1, macro approaches can be divided into three: one-fluid model, one-fluid/bubble model, and two-fluid model. The one-fluid model is a method to analyze by approximating the cavitation flow by a homogeneous medium flow (pseudo single-phase medium flow). In the one-fluid/bubble model, the liquid is solved as fluid, and the transport equation (Rayleigh-Plesset equation is an example of equation of motion of spherical bubbles in fluid) is solved for bubbles as an aggregation. In the two-fluid model, the liquid and the bubbles are analyzed as fluid respectively. Currently, many fluid simulation software products are using the one-fluid model with small calculation load. As shown is the example (hydrofoil) in Figure 2, the cavitation flow is analyzed by obtaining the void rate (gas phase volume fraction in a gas-liquid two-phase flow) distribution.

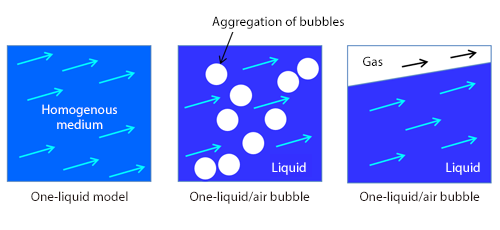
Figure 1: Macro approaches

Figure 2: Analysis example (hydrofoil)

The speed of sound of a liquid including bubbles is much smaller than that of the liquid itself. For example, the speed of sound of water is about 1500 m/s at 25°C, however, the speed of sound of water including bubbles with void rate of 0.2 is 30 m/s or less. In fluid simulation analyses, a flow that exceeds the speed of sound is called compressible flow and the density change is considered in a state equation. Therefore, to analyze a cavitation flow, local balance may be assumed in consideration of compressibility and the density change with the state equation of a gas-liquid two-phase medium may be considered. This kind of one-fluid model is called compressible local homogeneous medium model.

As a familiar example in our daily life, here is an example of cavitation generated when a hose is squeezed. As a child, you may have often played with a hose. When you squeeze a transparent hose with water running through, the water becomes clouded with a noise. This is because a negative pressure is generated by the increased flow rate in the part squeezed and the saturated vapor pressure is not reached locally, resulting in evaporation of water and occurrence of cavitation. This analysis was conducted by Keita Fujiyama in our Engineering Department.

Figure 3 shows an actual process to squeeze a hose, and the area in pink is the range of generation of bubbles caused by cavitation. You can see that the range of occurrence of cavitation spreads downstream as the hose is squeezed and it changes to periodic release of fine bubbles when the hose is squeezed further.

Figure 3: Occurrence of cavitation when hose is squeezed

Figure 4 shows analysis of occurrence of cavitation when the hose is kept significantly squeezed. The condition of the hose and the internal pressure fluctuation are shown in an animation by slowing down by 100 times. You can see from this result that very fine cavitation occurs when the flow route is narrowed by squeezing the hose and severe pressure fluctuation occurs with this. You can hear this change as noise. This animation has noise reproduced from the pressure fluctuation. It is difficult to reproduce noise same as the actual one, however, please listen to it because it is reproduced as noise with high frequency caused by occurrence of cavitation.

Figure 4: Occurrence of cavitation and internal pressure fluctuation when hose is squeezed significantly

About the Author 
Katsutaka Okamori | Born in October 1966, Tokyo, Japan

He attained a master’s degree in Applied Chemistry from Keio University. As a certified Grade 1 engineer (JSME certification) specializing in multi-phase flow evaluation, Okamori contributed to CFD program development while at Nippon Sanso (currently TAIYO NIPPON SANSO CORPORATION). He also has experience providing technical sales support for commercial software, and technical CFD support for product design and development groups at major manufacturing firms. Okamori now works as a sales engineer at Software Cradle.

About the Author
Keita Fujiyama | Born in December 1980, Kanagawa, Japan

Having attended Graduate School of Frontier Sciences in the University of Tokyo and attained master’s degree, where he became familiar with fluid experiments (in undergraduate studies) and superconductivity experiments (in graduate studies), he has worked for Dome Co., Ltd. and participated in design, development and wind tunnel experiments of racing cars. He currently works as a Software Cradle consulting engineer, and helps users solve complex CFD analysis problems that involve air and water.