Column: CFD basics02
New order | Old order


Want to Know More! Basics of Thermo-Fluid Analysis 19: Chapter 3 Flow 3.4.2 Laminar flow and turbulent flow (1)

Want to Know More! Basics of Thermo-Fluid Analysis 18: Chapter 3 Flow 3.4.1 Steady-state flow and transient flow

Want to Know More! Basics of Thermo-Fluid Analysis 17: Chapter 3 Flow 3.3.2 Compressibility and incompressibility (2)

Want to Know More! Basics of Thermo-Fluid Analysis 16: Chapter 3 Flow 3.3.2 Compressibility and incompressibility (1)

Want to Know More! Basics of Thermo-Fluid Analysis 15: Chapter 3 Flow 3.3.1 Viscosity and non-viscosity

Want to Know More! Basics of Thermo-Fluid Analysis 14: Chapter 3 Flow 3.2.3 Streamline, streakline, and pathline

Want to Know More! Basics of Thermo-Fluid Analysis 13: Chapter 3 Flow 3.2.2 Pressure

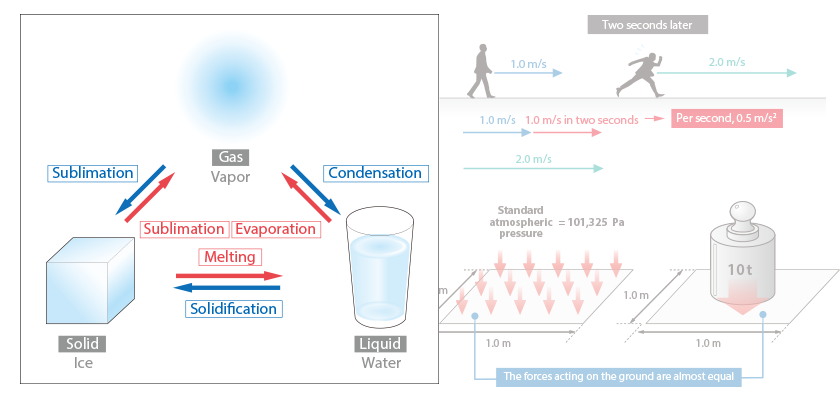
Want to Know More! Basics of Thermo-Fluid Analysis 12: Chapter 3 Flow 3.2.1 Velocity, speed, flow rate, and acceleration

Want to Know More! Basics of Thermo-Fluid Analysis 11: Chapter 3 Flow 3.1 Framework of Fluid Dynamics
Picked Up Contents
Whitepaper
Turbocharging CFD with Katana
Unleashing cutting-edge computational fluid dynamics from Japan


