Want to Know More! Basics of Thermo-Fluid Analysis 20: Chapter 3 Flow 3.4.2 Laminar flow and turbulent flow (2)
3.4.2 Laminar flow and turbulent flow (2)
Change in the flow condition from laminar to turbulent is called transition , and that from turbulent to laminar is called reverse transition . In addition, Reynolds number of flow at the transition boundary is called the critical Reynolds number .
The critical Reynolds number is not constant but varies depending on the turbulence of flow and the surface roughness of an object. Besides, the Reynolds number of a flow in transition from laminar to turbulent with the increase of velocity is different from that in reverse transition from turbulent to laminar with the decrease of velocity.
Last, let us calculate the Reynolds number of a flow seen in our daily lives. Here, we consider a car traveling at 50 km/h (= 13.89 m/s) as shown in Figure 3.30.
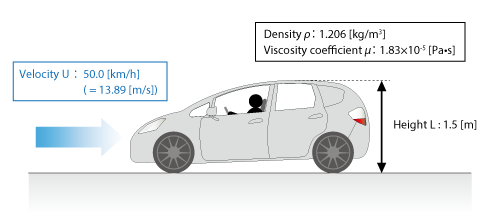
Figure 3.30 Flow around a car body
Substitute the velocity to the equation described in the previous column.
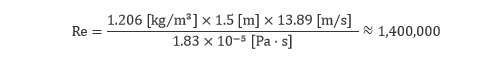
We can see that the Reynolds number reaches approximately 1.4 million. Because of its complicated shape, it is difficult to know the critical Reynolds number of a car; however, the equation shows the Reynolds number is very large and thus the flow is turbulent. This is just one example, and a major part of flows seen in our daily lives and in industrial scenes is turbulent flow.
Want to know more Charecteristic length and characteristic velocity
To compare two Reynolds numbers, the definitions of characteristic length and characteristic velocity must be the same between the (Reynolds number) calculations.
For example, it is known that the critical Reynolds number of flow in a cylinder is approximately 2,300. The value is obtained from the equation with the diameter of the cylinder as charecteristc length and the average velocity in the cylinder as characteristic velocity. If the radius of the cylinder is used as characteristic length, the value becomes approximately 1,150. As just described, the value of Reynolds number varies depending on the definitions of characteristic length and characteristic velocity.
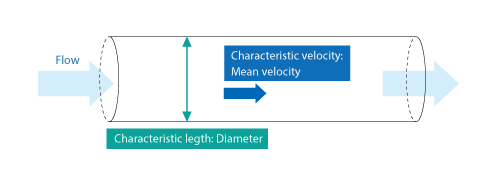
Figure 3.31 Definitions for Reynolds number of flow inside a cylinder
Note that the critical Reynolds number 2,300 is for the flow inside a cylinder, and the definitions for Reynolds number and the value of the critical Reynolds number vary depending on subjects. The critical Reynolds number 2,300 is not for all flow fields.
Want to know more Reynolds' law of similarity
Reynolds number represents the ratio of inertial force and viscous force. Therefore, if the shapes of two flow fields are similar and their Reynolds numbers are equal, the flows can be regarded as essentially the same. This is called Reynolds' law of similarity .
If a product and its model used for experiments are different in size, comparing the flows is difficult; however, Reynolds' law of similarity helps us understand correspondence between them.
See Figure 3.32. Assuming that a car travels at U [m/s], let us think about the velocity U’ [m/s] to simulate the flow around the car by using its model of 1/2 in size.
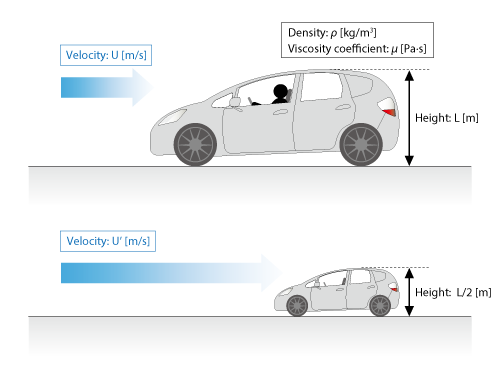
Figure 3.32 Flows around a car and around its model
If the Reynolds numbers of the two are equal, the following equation can be true.
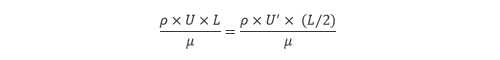
From the equation, the expression U'=2U is obtained. Then, we can see that the velocity of the 1/2 model must be double of the car velocity to simulate the flow around the car using the model.
Want to know more Dimensionless number
Indipendent basic seven factors to express physical quantities are called dimensions . The dimensions greatly related to thermo-fluid analyses are length “L”, mass “M”, time “T”, and temperature “Θ”. For example, area is given by the square of the length and has a dimension of “L2”. In the same manner, velocity is given by distance divided by time and has a dimension of “LT-1”.
Here, let us see the dimension of Reynolds number and Knudsen number described in 3.1. In the formula of each number, the unit is canceled between its denominator and its numerator. Thus, they have no dimension. This kind of parameter is called a dimensionless number . By using a dimensionless number, a phenomenon can be expressed without depending on a unit or a value as by Reynolds' law of similarity.

About the Author
Atsushi Ueyama | Born in September 1983, Hyogo, Japan )
He has a Doctor of Philosophy in Engineering from Osaka University. His doctoral research focused on numerical method for fluid-solid interaction problem. He is a consulting engineer at Software Cradle and provides technical support to Cradle customers. He is also an active lecturer at Cradle seminars and training courses and the author of serial articles Basic Course of Thermo-Fluid Analysis.


