3.3 Properties of fluids

3.3.1 Viscosity and non-viscosity

Real fluids have viscous. Thus, if a force act on a fluid, the force resistant to the applied force acts. This property of fluids is called viscosity and a fluid with viscosity is called viscous fluid. On the other hand, a virtual fluid without viscosity is called non-viscous fluid.

To consider a force caused by viscosity, let us think a flow of a fluid between two plates as shown in Figure 3.17. The flow is called Couette flow.

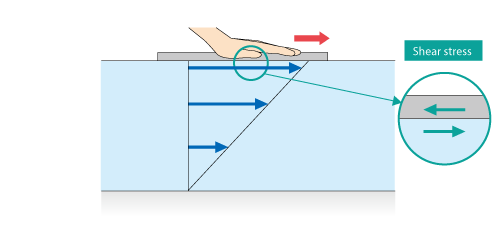
Figure 3.17　Couette flow

When the upper plate is moved to the right, a force is caused by viscosity. A force acts on the plate in the direction disturbing the force caused by viscosity; i.e., the force acts in the left direction. On the other hand, because a fluid under the upper plate is dragged with the plate, a force acts in the right direction. A force parallel to a plane is called shear force and its unit is N. A force acting per unit area is called stress and its unit is Pa. A shear force per unit area is called shear stress. Especially, a shear stress caused by fluid viscosity is sometimes called viscous stress.

In many fluids, shear stress τ acting on a plate is proportional to velocity gradient ∂u/∂y of a fluid and the proportionality factor corresponds to viscosity coefficient μ. Their relationship is expressed in the following equation.

The relationship is called Newton's law of viscosity and a fluid which obeys the law is called Newtonian fluid. Air and water can be considered Newtonian.

 Want to know more  Non-Newtonian fluid
A fluid which does not obey Newton’s law of viscosity is called a non-Newtonian fluid. Non-Newtonian fluids are classified into three types based on their characteristics: Bingham fluid, pseudoplastic fluid, and dilatant fluid. The relations between velocity gradient and shear stress of each fluid are shown in Figure 3.18.

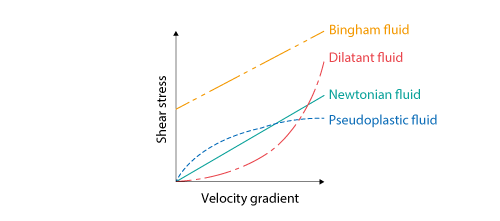
Figure 3.18 Relations between velocity gradient and shear stress of each fluid

As for a Bingham fluid, shear stress acts even when a Bingham fluid remains stationary. Thus, a Bingham fluid does not flow until shear stress reaches a certain value, and starts to flow when shear stress exceeds a certain value. The shear stress when a Bingham fluid starts to flow is called Bingham yield value. Toothpaste and butter are familiar examples of Bingham fluids.

For a pseudoplastic fluid, as velocity gradient gets greater, a velocity coefficient gets smaller and a pseudoplastic fluid flows easier. Ketchup is a familiar example of pseudoplastic fluids. Because of the property of a pseudoplastic fluid, we can easily take them out from a tube container.

A dilatant fluid has an opposite property to that of a pseudoplastic fluid. As velocity gradient gets greater, a velocity coefficient also gets greater and a dilatant fluid becomes harder to flow. A 1:1 mixture of water and starch is a typical dilatant fluid. When the mixture is quickly stirred, it becomes thicker and more difficult to stir.

About the Author
Atsushi Ueyama | Born in September 1983, Hyogo, Japan ）

He has a Doctor of Philosophy in Engineering from Osaka University. His doctoral research focused on numerical method for fluid-solid interaction problem. He is a consulting engineer at Software Cradle and provides technical support to Cradle customers. He is also an active lecturer at Cradle seminars and training courses and the author of serial articles Basic Course of Thermo-Fluid Analysis.