Want to Know More! Basics of Thermo-Fluid Analysis 12: Chapter 3 Flow 3.2.1 Velocity, speed, flow rate, and acceleration
3.2 Representation of flows
3.2.1 Velocity, speed, flow rate, and acceleration
Velocity and speed are a distance that a fluid or an object moves per unit time, and their unit is m/s. Velocity indicates the distance and the direction of a motion, and is called a vector quantity. To define a vector quantity, both magnitude and direction are needed. On the contraryother hand, speed indicates only the distance of a motion, but not the direction. This type of physical quantity is called scalar quantity. Table 3.1 shows some examples of vector and scalar quantities observed in thermo-fluid analyses even though some of them have not been introduced yet in the column series.
| Vector quantity | Scalar quantity | |
|---|---|---|
| Flow | Velocity, acceleration | Speed, pressure |
| Heat | Heat flux | Temperature |
| Diffusion | Diffusion flux | Concentration |
Let us take Figure 3.4 for example; two people walk at 1.0 m/s, one north and the other south. Assume that north is the positive direction. The one who walks north goes the positive direction, thus his velocity is represented as +1.0 m/s, and for the other who walks south, the velocity is represented as -1.0 m/s because south is the negative direction. As for speed, both walk at 1.0 m/s equally without consideration of direction. Note that, as shown above, even if the speed is the same, the velocity varies depending on the direction.
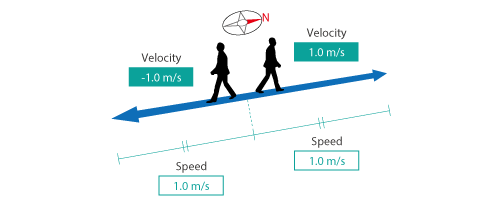
Figure 3.4 Difference between velocity and speed
Volume flow rate is the volume of a fluid passing through per unit time, and its unit is m3/s. Volume flow rate is obtained by multiplying the area of a reference surface plane by the speed of the flow perpendicular to the surfaceplane. Mass flow rate is the mass of a fluid passing through per unit time, and its unit is kg/s. When the density of a fluid is constant, the mass flow rate is obtained by multiplying the volume flow rate by the density of a fluid. The word flow rate generally means volume flow rate.
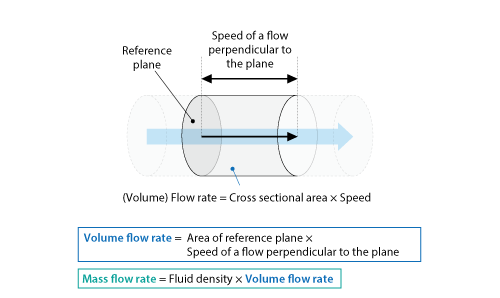
Figure 3.5 Volume flow rate and mass flow rate
Acceleration is the rate of change of the velocity of a fluid or an object per unit time, and its unit is m/s2. Let us take Figure 3.6 for example. If someone walking at 1.0 m/s increases his pace to 2.0 m/s two seconds later, the velocity changes 1.0 m/s in two seconds; i.e., the acceleration per second is 0.5 m/s2. Note that, if he decreases his pace, the acceleration will be a negative value.
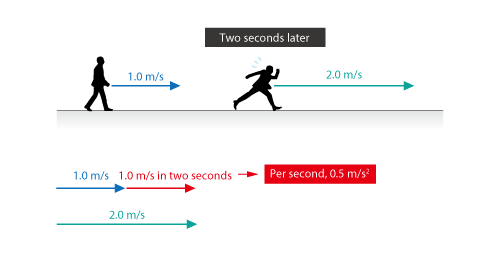
Figure 3.6 Basics of acceleration
Want to know more Components of a vector
Vector quantity has a concept, “components”. Let us take a 2D velocity vector shown in Figure 3.7 for example.
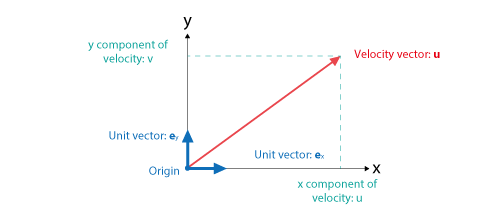
Figure 3.7 Velocity vector and its components
As shown in the figure, a velocity vector can be decomposed into two components; x and y directions. The negative and positive measurements from the origin in each direction are called components and described as (u, v). A vector of length unity in each direction is called unit vector. Assuming that unit vectors in x and y directions are expressed as ex and ey respectively, the following relation can be obtained between the velocity vector and each component.
u = u ex + v ey
Want to know more Eulerian method and Lagrangian method
To observe a fluid motion, we have two methods: Eulerian method and Lagrangian method. In Eulerian method, a flow is observed from a point fixed in a space. In Lagrangian method, on the other hand, a flow is observed from a point moving with the flow.
Seeing Figure 3.8, let us think about observation of the velocity of a car. The observer is standing on the road in Eulerian method, while he is sitting in the front passenger seat in Lagrangian method.
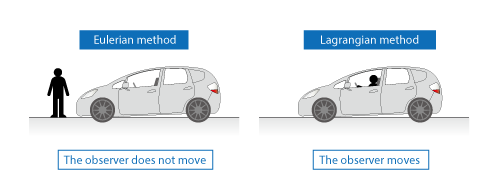
Figure 3.8 Eulerian method and Lagrangian method
Among thermo-fluid analyses, using mesh fixed in a space to observe a flow is in the category of Eulerian method. In the particle method, on the other hand, each particle is an observation point following a flow, and the method is in the category of Lagrangian method. In addition, the ALE method stands on the middle of the two methods.

About the Author
Atsushi Ueyama | Born in September 1983, Hyogo, Japan )
He has a Doctor of Philosophy in Engineering from Osaka University. His doctoral research focused on numerical method for fluid-solid interaction problem. He is a consulting engineer at Software Cradle and provides technical support to Cradle customers. He is also an active lecturer at Cradle seminars and training courses and the author of serial articles Basic Course of Thermo-Fluid Analysis.


