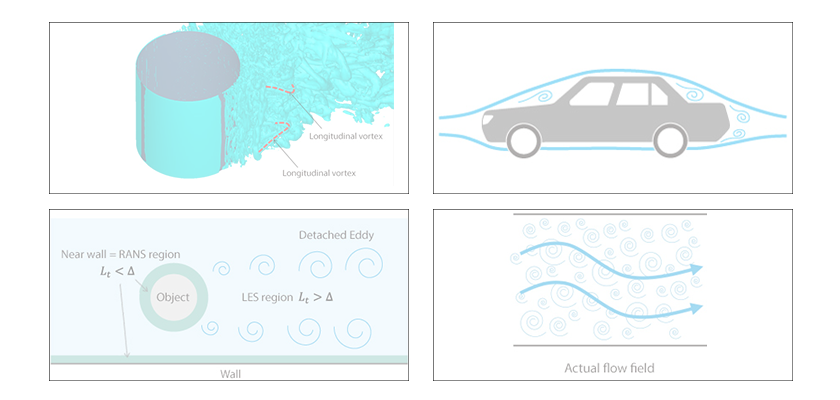
Laminar flow or turbulent flow

18.1: Estimating Reynolds number

So far, we have learned the mechanisms and calculation methods of turbulent flow. In this column, we will learn about Reynolds number, which is used to determine whether we should treat a flow as laminar flow or turbulent flow. Reynolds number Re is calculated as:

Re＝(Fluid density · Characteristic velocity · Characteristic length / Fluid viscosity)

It is also explained as being the ratio between inertia force and viscous force of fluid. There should be no controversy about density and viscosity, which are dictated by the type of fluid. The factors ‘characteristic velocity’ and ‘characteristic length’, however, make us puzzle over how they should be determined because they depend on the situations of the flow of interest. You can think of the word ‘characteristic’ here as something that “characterizes” the flow to be simulated, or the flow of interest. Let us see an example of how to determine the characteristic velocity and characteristic length. For a flow around a ball shown in Figure 18.1, inflow velocity U is the characteristic velocity and the ball diameter D is the characteristic length. If, however, the ball is a golf ball and if we like to focus on one of the dimples for a detailed calculation, then the characteristic length would be either the depth or the diameter of the dimple as shown in Figure 18.2.

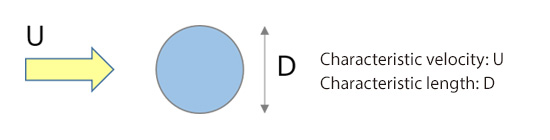
Figure 18.1: Characteristic velocity and characteristic length for a flow around a ball

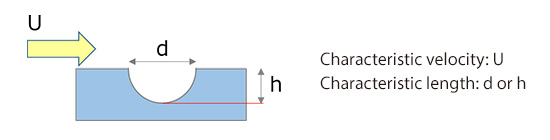
Figure 18.2: Characteristic velocity and characteristic length for a flow around a dimple

If there are multiple objects with different sizes in the flow as shown in Figure 18.3, you may wonder which length should be selected as the characteristic length. A common practice is to take the longest among them as the characteristic length. Anyhow, an estimate of the order of magnitude is good enough for Reynolds number; therefore, we can also say that it is fine to use any of the lengths as the characteristic length as long as their sizes are not largely different.

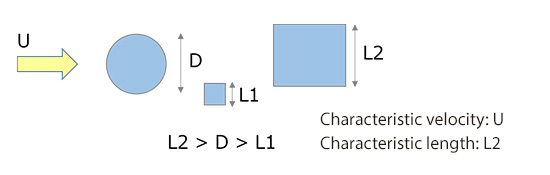
Figure 18.3: Characteristic velocity and characteristic length for a flow with multiple objects

Let us see another example. It is a flow analysis in which an object is placed inside a duct as shown in Figure 18.4. The characteristic length can be selected from the object height h or the duct diameter D. Although the object height h seems suitable when we focus only on the object, the duct diameter D should be selected because that is what “characterizes” the flow upstream of the object.

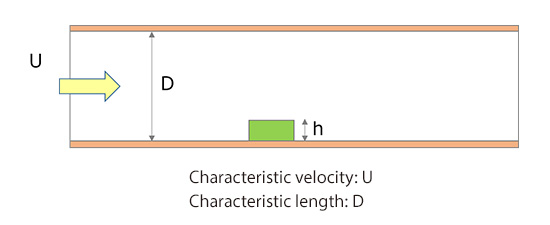
Figure 18.4: Characteristic length in an internal flow

We have learned how to estimate Reynolds number through four examples. All in all, there is no absolute principle in estimating Reynolds number, and some ambiguity remains. I hope you have grasped the overall picture of Reynolds number estimation from these examples. In the next column, we will discuss another familiar phenomenon.

About the Author
Takao Itami | Born in July 1973, Kanagawa, Japan

The author had conducted researches on numerical analyses of turbulence in college. After working as a design engineer for a railway rolling stock manufacturer, he took the doctor of engineering degree from Tokyo Institute of Technology (Graduate School of Science and Engineering) through researching compressible turbulent flow and Large-Eddy Simulation. He works as a consulting engineer at Software Cradle solving various customer problems with his extensive experience.