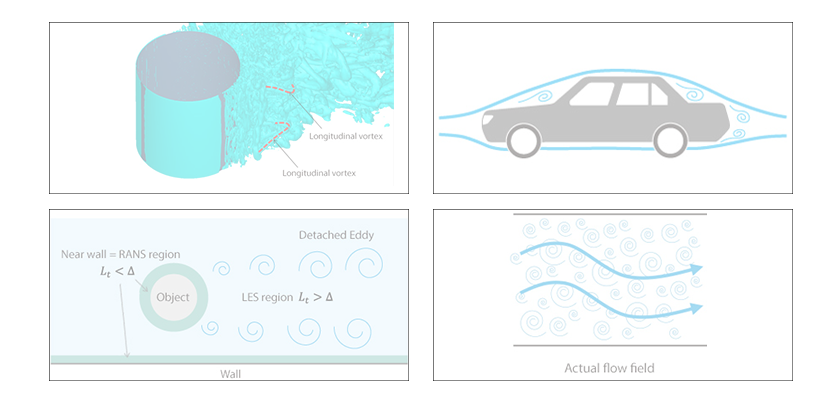
Methods of turbulent flow calculation (8) Hybrid model

14.1: Overview of hybrid model

We will discuss ‘hybrid model’ in this column. We have discussed three methods of turbulent flow calculation: DNS, RANS, and LES. DNS is a method only applicable to researches, and even LES has a computational load that is often too high to be practically usable. Thereupon ‘hybrid model’ was invented by combining RANS and LES. A hybrid model is a method to calculate some portion of computational domain with RANS model and the rest with LES. The intension of this is to calculate the portion of high computational load with RANS so that the total computational load is reduced, while retaining the advantages of LES. There are several hybrid models with different calculation methods. We will discuss Detached Eddy Simulation (DES) and Very Large Eddy Simulation (VLES) below.

14.2: Detached Eddy Simulation(DES)

The words ‘Detached Eddy’ stand for an ‘eddy that is apart from walls’. Eddies in turbulent flows are generated due to velocity gradient, and a wall is one of the places where eddies are generated. An eddy is generated due to velocity gradient, which is created by the presence of a wall, and drifts on the flow away from the wall; that is ‘Detached Eddy’ (Figure 14.1). DES is mainly designed to calculate this sort of eddies apart from walls. On the other hand, DES does not calculate small eddies near walls directly but calculates only the averaged field using RANS model. By doing so, mesh can be made coarse near walls where otherwise the finest mesh is required, which reduces the computational load compared to LES. It has been commented, however, that DES may not be capable of simulating the most important portion, namely the places for generation of eddies, because it relies on RANS near walls.

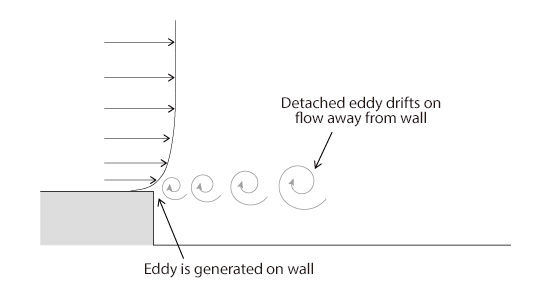
Figure 14.1: Detached Eddy

In DES, RANS and LES are switched from one another by using an index for the size of eddies called ‘turbulent length scale’. Turbulent length scale is a value calculated using turbulent energy k and turbulent dissipation rate ε as follows:

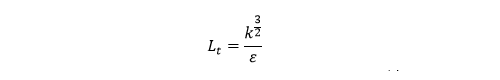
If this turbulent length scale is smaller than mesh size, RANS calculation is performed, and if it is larger than mesh size, LES calculation is performed. Technically, ‘LES calculation’ in this context is not the same as LES; rather, it is “similar” to LES. As described above, the sizes of eddies become small near walls, which leads to RANS calculation. Conversely, for the regions with large eddies apart from walls, LES calculation is performed for Detached Eddies (Figure 14.2).

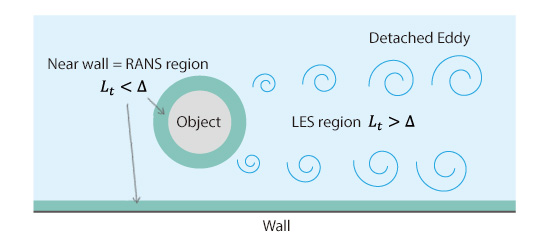
Figure 14.2: Illustration of DES

14.3: Very Large Eddy Simulation (VLES)

The words ‘Very Large Eddy’ stand for the concept of calculating only very large eddies among eddies calculated in LES. The basic way of thinking is the same as that of DES; RANS model is used for the calculation near walls, where LES requires finer mesh, and the rest is calculated with LES. The switching methods between RANS and LES, however, are different. We will learn two methods here. The first method is the one that uses a space filter proposed by Ruprecht and others. As shown in Figure 14.3, this method applies a mesh-sized filter to the turbulent energy calculated in RANS equations, and calculates eddy viscosity by using only the turbulent energy left after filtering, i.e., only the turbulent energy regarding the eddies smaller than mesh size. This process restrains eddy viscosity acting on large eddies that can be captured with the mesh size and makes it possible to capture (unsteady) vortex motions within that size.

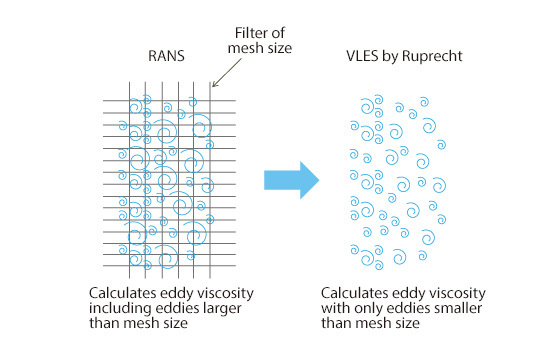
Figure 14.3: VLES by Ruprecht and others

The second method is the one proposed by Batten and others, and it switches between RANS and LES according to the magnitude relation between eddy viscosities in each of them. The definitions of eddy viscosities in RANS and LES are the following:

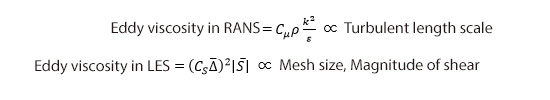
where, Cμ and CS are model constants, ρ is fluid density, 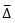 is filter size,  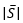is magnitude of shear. Eddy viscosity in RANS is proportional to turbulent length scale, whereas eddy viscosity in LES is proportional to filter size, i.e., mesh size, and magnitude of shear. In the method by Batten and others, if viscosity of RANS is larger than that of LES, then eddy viscosity of LES is adopted; that is, LES calculation is performed. Conversely, if eddy viscosity of LES is larger, then RANS calculation is performed. Since eddy viscosity of LES is proportional to mesh size as described above, for an eddy of the same size (turbulent length scale), coarse mesh leads to RANS calculation, and fine mesh leads to LES calculation (Figure 14.4).

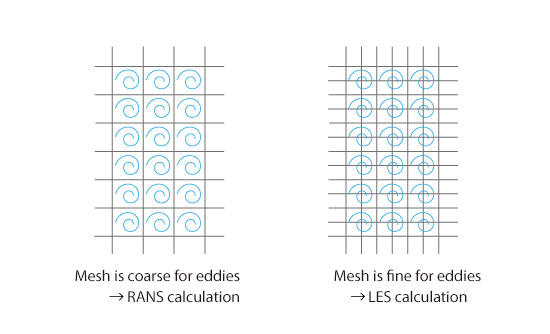
Figure 14.4: VLES by Batten and others

A common factor for both models is that they are trying to prevent vortex motions that can be captured with mesh size from disappearing (diffusing) by making the magnitude of eddy viscosity in fine-mesh regions smaller than in RANS model. In other words, when we divide a flow field into regions of vortices larger than mesh size and those smaller than mesh size, eddy viscosity will have a large value in RANS model regardless of the size of vortices because unsteady transient vortices are all modeled. On the contrary, vortices larger than mesh size are not modeled but calculated directly in LES. Eddy viscosity will have a small value because modeling is performed only for vortices smaller than mesh size. In these contexts, restraining eddy viscosity enables a calculation similar to LES.

In the next column, we will discuss sample calculations of hybrid model.  

---

About the Author
Takao Itami | Born in July 1973, Kanagawa, Japan

The author had conducted researches on numerical analyses of turbulence in college. After working as a design engineer for a railway rolling stock manufacturer, he took the doctor of engineering degree from Tokyo Institute of Technology (Graduate School of Science and Engineering) through researching compressible turbulent flow and Large-Eddy Simulation. He works as a consulting engineer at Software Cradle solving various customer problems with his extensive experience.