Basic Course on Turbulence and Turbulent Flow Modeling 5: 5.1 Turbulent flow and vortex tube, 5.2 Interaction between vortex tubes, 5.3 Kolmogorov’s similarity hypothesis
Mechanism of turbulent flow (2)
5.1 Turbulent flow and vortex tube
The previous column explained that velocity difference causes turbulent flow and that eddies are formed in the turbulent flow. When eddies are visualized, they look like tubes; therefore, the visualized eddies are called “vortex tubes”. Imagine that tubes are flowing in a turbulent flow. Figure 5.1 shows vortex tubes in a flow passing on a plate with a step. The size (diameter) of vortex tubes is various. Their shape is also various and you can see straight-line-shaped tubes, curved tubes, and tubes with different diameters. Reynolds number is different between the right and left figures shown below. Reynolds number in the right figure is higher. These figures show that when Reynolds number is higher, more vortex tubes are formed.
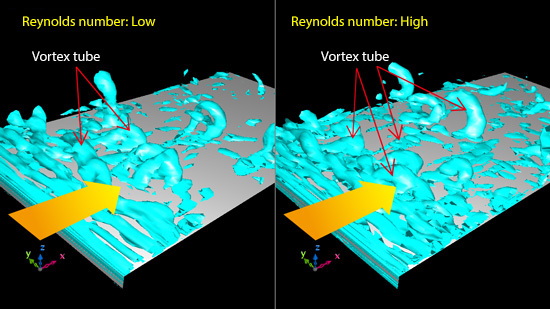
Figure 5.1: Image of vortex tubes in a turbulent flow
5.2 Interaction between vortex tubes
Vortex tubes are generated because of velocity difference in a flow. When a vortex tube is generated, it causes velocity difference in its neighboring regions. Then, the difference causes a new vortex tube. This interaction between vortex tubes is repeated and new vortex tubes are generated one after another. When a new vortex tube is generated, its diameter is the same as or smaller than that of the original vortex tube. (You can easily imagine that generating a larger one is difficult.) When a large vortex tube and a small vortex tube interact with each other, a vortex tube with medium-diameter may be generated. A new vortex tube does not always occur in the same direction with that of the original vortex tube, and some new tubes are perpendicular to their original. In this way, various vortex tubes are generated in a flow field. Figure 5.2 shows vortex tubes in a flow around a cylinder. Many vortex tubes are generated downstream of the cylinder; however, the directions of the vortex tubes are not uniform. When turbulent motion increases, a mass of vortex tubes which look random is formed.
Figure 5.2 Vortex tubes in a flow around a cylinder
5.3 Kolmogorov’s similarity hypothesis
Vortex tubes seem to be randomly generated by velocity difference and interaction between vortex tubes. However, when energy of each vortex tube in a flow field is classified per tube size, a fixed curve shown in Figure 5.3 is obtained. The horizontal axis of the graph indicates the inverse of the diameter of each vortex tube. The farther you go to the right on the horizontal axis, the smaller the vortex tube size is. The vertical axis indicates the energy that each vortex tube has. Both horizontal and vertical axes are logarithmic. This graph is characterized by a higher part on the left, lower part on the right, and straight part (because of logarithmic expression) in the middle. Interestingly, when a graph like Figure 5.3 is applied to vortex tubes in various flow fields according to the determined process, the curve from the straight line in the middle to the lower part on the right end is almost the same. The peak on the left side varies depending on Reynolds number and called “integral length”. The energy of the vortex tube with the diameter of the integral length comprises the majority of the energy of vortex tubes in a flow field. The slope of the straight line in the middle equals to -5/3 in logarithmic expression and all straight lines of turbulent vortex tubes are on the line. This is called “Kolmogorov -5/3 law”. “Kolmogorov” is the name of a Russian mathematician. The size of the right end indicates the smallest scale of vortex tubes and called “Kolmogorov scale”. Vortex tubes whose size is smaller than Kolmogorov scale do not exist. This is because the tubes disappear as they are converted to heat by the action of fluid viscosity. The movement of a turbulent flow (an assembly of vortex tubes) looks random. However, as shown in Figure 5.3, there is a law, which indicates that a turbulent flow is a well-ordered phenomenon. Then, this is one of the motivations to model a turbulent flow.
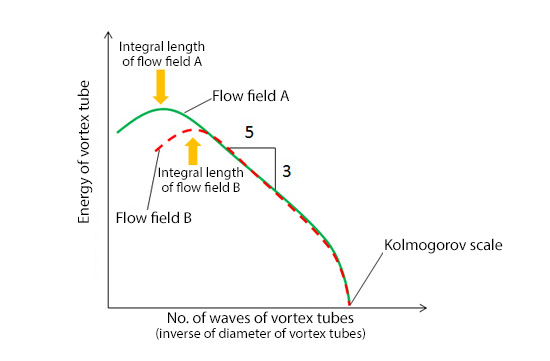
Figure 5.3: Kolmogorov’s similarity law

About the Author
Takao Itami | Born in July 1973, Kanagawa, Japan
The author had conducted researches on numerical analyses of turbulence in college. After working as a design engineer for a railway rolling stock manufacturer, he took the doctor of engineering degree from Tokyo Institute of Technology (Graduate School of Science and Engineering) through researching compressible turbulent flow and Large-Eddy Simulation. He works as a consulting engineer at Software Cradle solving various customer problems with his extensive experience.


